问题
计算题
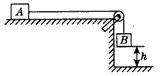
如图所示，在水平桌面的边角处有一轻质光滑的定滑轮，一条不可伸长的轻绳绕过定滑轮分别与物块A、B相连，轻绳处于伸直状态，物块A和B的质量分别为mA=8 kg和mB=2kg，物块A与水平桌面间的动摩擦因数μ=0.1，物块B距地面的高度h=0.15 m。桌面上的部分绳足够长。现将物块B从h高处由静止释放，直到A停止运动。求A在水平桌面上运动的时间？（g取10 m/s2）
答案
解：以物块B为研究对象，由牛顿第二定律得：mBg-F=mBa1
同理，对物块A：F-Ff=mAa1，Ff=μFNA，FNA-mAg=0
联立解得：a1=1.2 m/s2
B做匀加速直线运动，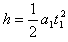
，v=a1t1，解得：t1=0.5 s，v=0.6 m/s
B落地后，A在摩擦力作用下做匀减速运动，Ff=mAa2，t2=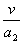
，解得：t2=0.6 s
故A运动的时间为t=t1十t2=1.1 s