问题
计算题
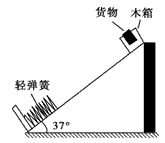
如图所示为某同学设计的节能运输系统。斜面轨道的倾角为37°,木箱与轨道之间的动摩擦因数μ=0.25。设计要求:木箱在轨道顶端时,自动装货装置将质量m=2 kg的货物装入木箱,木箱载着货物沿轨道无初速滑下,当轻弹簧被压缩至最短时,自动装货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端,接着再重复上述过程。若g取10 m/s2,sin37°=0.6 ,cos37°=0.8。求:
(1)离开弹簧后,木箱沿轨道上滑的过程中的加速度大小;
(2)满足设计要求的木箱质量。
答案
解:(1)设木箱质量为m′,对木箱的上滑过程,由牛顿第二定律有:
m′gsin 37°+μm′gcos 37°=m′a
代入数据解得:a=8 m/s2
(2)设木箱沿轨道下滑的最大距离为L,弹簧被压缩至最短时的弹性势能为Ep,根据能量守恒定律:
货物和木箱下滑过程中有:(m′+m)gsin37°L=μ(m′+m)gcos37°L+Ep
木箱上滑过程中有Ep=m′gsin37°L+μm′gcos37°L
联立代入数据解得:m′=m=2 kg
