问题
计算题
A,B两个木块叠放在竖直轻弹簧上,如图所示,已知mA=mB=1 kg,轻弹簧的劲度系数为100 N/m。若在木块A上作用一个竖直向上的力F,使木块A由静止开始以2 m/s2的加速度竖直向上做匀加速运动,取g=10 m/s2,求:
(1)使木块A竖直向上做匀加速运动的过程中,力F的最大值是多少?
(2)若木块A竖直向上做匀加速运动,直到A,B分离的过程中,弹簧的弹性势能减小了1.28 J,则在这个过程中,力F对木块做的功是多少?
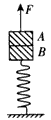
答案
解:(1)F-mAg+FA=mAa,所以当FBA=0时,F最大,即Fm=mAg+mAa=12 N
(2)初始位置弹簧的压缩量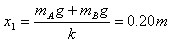
A,B分离时,FAB=0,以B为研究对象可得FN-mBg=mBa,FN=12 N
此时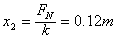
A,B上升的高度:△x=x1-x2=0.08 m
A,B的速度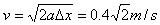
以A,B作为一个整体,由动能定理得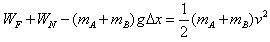
可得WF=0.64 J
