图l中,质量为m的物块叠放在质量为2m的足够长的木板上方右侧,木板放在光滑的水平地面上,物块与木板之间的动摩擦因数为μ=0.2。在木板上施加一水平向右的拉力F,在0~3s内F的变化如图2所示,图中F以mg为单位,重力加速度g=10m/s2。整个系统开始时静止。
(1)求1s、1.5s、2s、3s末木板的速度以及2s、3s末物块的速度;
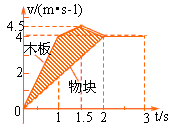
(2)在同一坐标系中画出0~3s内木板和物块的v-t图象,据此求0~3s内物块相对于木板滑过的距离。
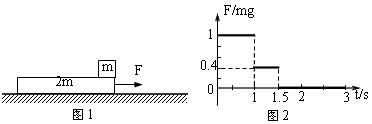
解:(1)设木板和物块的加速度分别为a和a',在t时刻木板和物块的速度分别为vt和vt',木板和物块之间摩擦力的大小为f,依牛顿第二定律、运动学公式和摩擦定律得
f=ma' ①
f=μmg,当vt' <vt ②
vt2'=vt1'+a'(t2-t1) ③
F-f=2ma ④
vt2=vt1+a(t2-t1) ⑤
由①②③④⑤式与题给条件得v1=4m/s,v1.5=4.5m/s,v2=4m/s,v3=4m/s ⑥
v2'=4m/s,v3'=4m/s ⑦
(2)由⑥⑦式得到物块与木板运动的v-t图象,如图所示。在0~3s内物块相对于木板的距离△s等于木板和物块v-t图线下的面积之差,即图中带阴影的四边形面积,该四边形由两个三角形组成,上面的三角形面积为0.25(m),下面的三角形面积为2(m),因此△s=2.25m ⑧