问题
计算题
在光滑的水平轨道上有两个半径都是r的小球A和B,如图所示,质量分别为m和2m,当两球心间距离大于l(l比2r大得多)时,两球之间无相互作用力;当两球心间的距离等于或小于l时,两球间存在相互作用的恒定斥力F,设A球从远离B球处以速度v0沿两球连心线向原来静止的B球运动,如图所示,欲使两球不发生接触,v0必须满足的条件?
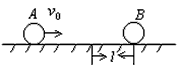
答案
解:A球开始做匀速直线运动,直到与B球接近至l时,开始受到与v0反向的恒力而做匀减速直线运动。B球则从A与其相近至l开始,受到与v0同方向的恒力,做初速度为零的匀加速直线运动。两球间距离逐渐变小。两球不发生接触的临界条件是:两球速度相等时,两球间的距离最小,且此距离必须大于2r。即
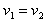 ①
①
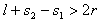 ②
②
其中v1,v2为当A、B两球距离最小时,A、B两球的速度;s1,s2为两球间距离从l变到最小的过程中A、B两球通过的路程
由牛顿第二定律可得,A球在减速运动,B球在加速运动的过程中,A、B两球的加速度大小为:
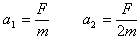
将a1,a2代入运动学公式,可得
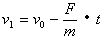 ③
③
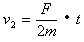 ④
④
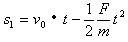 ⑤
⑤
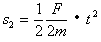 ⑥
⑥
上述6式联立解得