问题
计算题
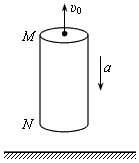
如图所示，离地面足够高处有一竖直的空管，质量为2kg，管长为24m，M、N为空管的上、下两端，空管受到F=16N竖直向上的拉力作用，由静止开始竖直向下做加速运动，同时在M处一个大小不计的小球沿管的轴线竖直上抛，小球只受重力，取
。求：
（1）若小球上抛的初速度为10m/s，经过多长时间从管的N端穿处。
（2）若此空管的N端距离地面64m高，欲使在空管到达地面时小球必须落到管内，在其他条件不变的前提下，求小球的初速度大小的范围。
答案
解：（1）取向下为正，小球初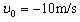速度
，加速度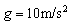
对空管，由牛顿第二定律可得：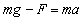
解得：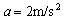
设经t时间，小球从N端穿出，小球下落的高度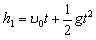
空管下落的高度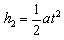
则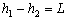
即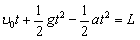
代入数据解得：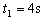
，
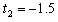s（舍）
（2）设小球初速度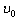
，空管经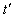
时间到达地面，则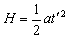
解得：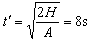
小球在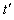
时间下落高度为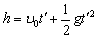
小球落入管内的条件是64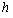m≤
≤88m
解得：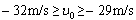
所以小球的初速度大小必须在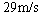
到
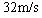范围内
