问题
计算题
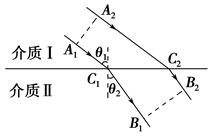
如图所示，一列平面波朝着两种介质的界面传播，A1A2是它在介质Ⅰ中的一个波面，C1和C2位于两种介质的界面上，B1B2是这列平面波进入介质Ⅱ后的一个波面；A1C1和A2C2是它的两条波线，入射角为θ1，折射角为θ2，波在Ⅰ、Ⅱ介质中的传播速度分别为v1和v2.
(1)试根据惠更斯原理证明：
＝
；
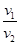(2)若已知θ1＝53°(sin 53°＝0.8)，A1A2的长度为0.6 m，介质Ⅰ和介质Ⅱ中的波速之比为v1∶v2＝4∶3，则：A1C1B1与A2C2B2的长度相差多少？
答案
(1)见解析(2)0.2 m
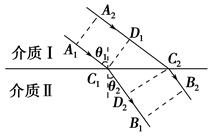
(1)证明：如图，根据惠更斯原理画出波面C1D1与C2D2
在Rt△C1D1C2和Rt△C2D2C1中：∠C2C1D1＝θ1，∠C1C2D2＝θ2，有：
sin θ1＝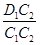
sin θ2＝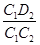
又因为D1C2＝v1t
C1D2＝v2t
所以联立各式得：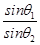
＝
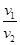得证．
(2)根据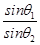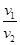＝，v1∶v2＝4∶3和θ1＝53°得：θ2＝37°
所以C1C2＝1.0 m，D1C2＝0.8 m，C1D2＝0.6 m，所以A1C1B1与A2C2B2的长度相差Δr＝ D1C2－ C1D2＝0.2m.