问题
计算题
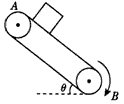
如图所示,A、B两轮间距l=3.25 m,套有传送带,传送带与水平面成θ=30°角,轮子转动方向如图所示,使传送带始终以2 m/s的速度运行,将一物体无初速度地放到A轮处的传送带上,物体与传送带间的动摩擦因数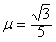 ,求物体从A运动到B所需的时间。(g取10 m/s2)
,求物体从A运动到B所需的时间。(g取10 m/s2)
答案
解:刚将物体由静止放上传送带时,摩擦力提供动力,如图甲所示,由牛顿第二定律得:
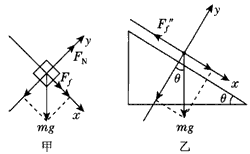
在x轴方向:mgsin30°+Ff=ma1 ①
在y轴方向:FN-mgcosθ=0 ②
摩擦力公式Ff=μFN ③
由①②③式得a1=g(sin30°+μcos30°)=8.0 m/s2
故有:第一阶段加速的时间为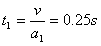
第一阶段物体的位移为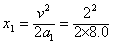 m=0.25 m
m=0.25 m
当物体在第二阶段中与传送带具有共同速度时,所受摩擦力Ff'=0,又由于mgsin30°>μmgcos30°,故物体仍会继续加速下滑,而摩擦力方向变为沿斜面向上,受力如图乙所示,由牛顿第二定律可得:
x轴方向上:mgsin30°-Ff''=ma2 ④
y轴方向上:FN-mgcos30°=0 ⑤
摩擦力公式:Ff''=μFN ⑥
由以上三式得:a2=g(sin30°-μcos30°)=2.0 m/s2
因而,在第二阶段物体以v=2 m/s和a2=2.0 m/s2做匀加速运动,其位移为:x2=l-x1=3.25 m-0.25 m=3.0 m
由位移公式得x2=vt2+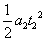 ,代入数值得:3=2×t2+
,代入数值得:3=2×t2+ ×2t22,解得t2=1 s
×2t22,解得t2=1 s
故所用总时间为t=t1+t2=0.25 s+1 s=1.25 s