问题
计算题
消防队员为了缩短下楼的时间,往往抱着固定在水平地面上的竖直杆直接滑下。训练中一名质量为60 kg的消防队员从离地面12.5 m的高度抱着杆以最短的时间滑下,要求消防队员落地的速度不能大于5 m/s。已知该消防队员对杆的最大压力为1800 N,他与杆之间的动摩擦因数为0.5。(重力加速度g=10 m/s2)求:
(1)消防队员下滑过程中的最大速度和达到最大速度时所用的时间各是多大?消防队员下滑到地面所用的最短时间是多大?
(2)若竖直杆的质量为200 kg,请在图中作出杆对地面的压力随时间变化的图像。
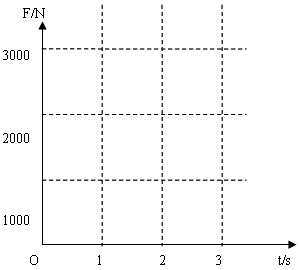
答案
解:(1)欲使滑下的时间最短,消防队员开始做自由落体运动,然后手和脚以最大的压力抱紧杆向下做匀减速运动,设消防员做自由落体运动的时间为t1,最大速度为v1,下落的高度为s1,根据运动学公式有
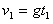
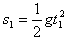
消防员做减速运动的时间为t2,加速度大小为a,下降的高度为s2,根据牛顿第二定律和运动学公式有
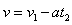
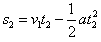
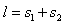
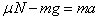
联立方程代入数据解得:t1=1s,t2=1s
最短时间t=t1+t2=2s
(2)在t1时间内,因为消防队员做自由落体运动,消防队员对杆没有作用力,所以杆对地面的压力等于杆的重力,即为:N1=Mg=200×10N
在t2时间内,根据力的平衡条件和牛顿第三定律,杆对地面的压力为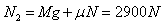
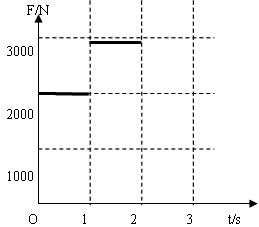
杆对地面的压力随时间变化的图像如图所示