问题
计算题
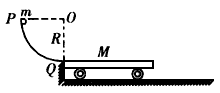
如图所示,一辆质量为M=2 kg、长L=2. 25 m的小车放在光滑水平面上。小车的左端上表面与四分之一光滑网弧轨道PQ的底端Q相切,圆弧轨道的半径为R= 1.8 m、固定在竖直平面内。小车的上表面离地面高度为h=0.8 m。一质量为m=1 kg 的小物块从圆弧轨道顶端由静止开始滑下,最后从小车右端水平飞出,小物块与小车上表面的动摩擦因数为μ=0.4,g=10m/s2。求:
(1)小物块滑到圆弧轨道底端(最低点)Q时,对轨道的压力;
(2)小物块在小车上运动的时间;
(3)小物块落地的瞬时与小车右端的距离。
答案
解:
(1)设小物块滑到圆弧轨道底端Q的速度vQ,在小物块从圆弧轨道上滑下的过程中,由机械能守恒定律得
mgR=mvQ2/R
小物块在圆弧轨道底端Q,由牛顿第二定律有
N-mg=mvQ2/R
联立解出N=30 N
由牛顿第三定律,小物块对轨道的压力为30 N;
(2)小物块在小车上滑动过程中,小物块与小车加速度分别为am和aM,对地位移分别为xm和xM,则
am=μmg/m
aM=μmg/M
xm=vQt-amt2/2
xM=aMt2/2
又L=xm-xM
联立解出t=0.5 s
(3)小物块从小车右端水平飞出时,小物块与小车的速度分别为vm=vQ-amt
vM=aMt
又h=gt'2/2
x=(vm-vM)t'
联立解出x=1.2 m。
