问题
计算题
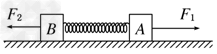
如图所示,在水平地面上有A、B两个物体,质量分别为mA=3.0 kg和mB=2.0 kg,它们与地面间的动摩擦因数均为μ=0.10。在A、B之间有一原长l=15 cm、劲度系数k=500 N/m的轻质弹簧将它们连接.现分别用两个方向相反的水平恒力F1、F2同时作用在A、B两物体上,已知F1=20 N,F2=10 N,取g=10 m/s2。当物体运动达到稳定时,求:
(1)A和B共同运动的加速度;
(2)A、B之间的距离(A和B均可视为质点).
答案
解:(1)A、B组成的系统在运动过程中所受摩擦力为Ff=μ(mA+mB)g=5.0 N
设运动达到稳定时系统的加速度为a,根据牛顿第二定律有F1-F2-Ff=(mA+mB)a
解得a=1.0 m/s2
(2)以A为研究对象,运动过程中所受摩擦力FfA=μmAg=3.0 N
设运动达到稳定时所受弹簧的弹力为FT,根据牛顿第二定律有F1-FfA-FT=mAa
解得FT=14 N
所以弹簧的伸长量△x=FT/k=2.8 cm
因此运动达到稳定时A、B之间的距离为x=l+△x=17.8 cm
