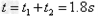问题
计算题
如图所示，将斜面体固定在水平面上，其两个斜面光滑，斜面上放置一质量不计的柔软薄纸带。现将质量为mA的A物体和质量为mB的B物体轻放在纸带上。两物体可视为质点，物体初始位置及数据如图所示。
（1）若纸带与物体A、B间的动摩擦因数足够大，在纸带上同时放上A、B后，发现两物体恰好都能保持静止，则mA和mB应满足什么关系?
（2）若mA=2 kg，mB=1 kg，A与纸带间的动摩擦因数μA=0.5，B与纸带间的动摩擦因数μB=0.8，假设两物体与纸面间的滑动摩擦力与最大静摩擦力相等，试通过计算简要描述两物体同时从静止释放后的运动情况，并求出B物体自释放起经过多少时间到达斜面底端。（sin37°=0.6，cos37°=0.8，g取10 m／s2）
答案
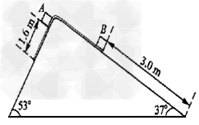
解：（1）纸带处于平衡态，说明A、B两物体对纸带的静摩擦力大小相等，则
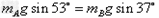
解得：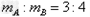
（2）假设纸带固定不动，对A物体受力分析得：
，则A相对纸带滑动
对B物体受力分析得：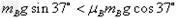
，则B相对纸带不滑动
对B和纸带整体分析，A对纸带的滑动摩擦力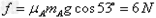
B的重力沿斜面分力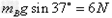
则说明若A、B和纸带同时释放后，B和纸带先静止不动，A沿纸面加速下滑1.6m后，B再拖动纸带一起沿光滑斜面加速下滑
A沿带纸下滑过程中：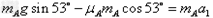
B拖动纸带一起沿光滑斜面加速下滑过程中：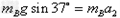
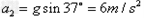
则所求总时间