问题
问答题
如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,
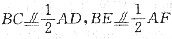 ,G,H分别为FA,FD的中点.
,G,H分别为FA,FD的中点.
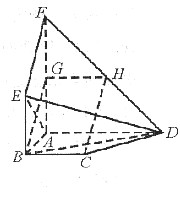
C,D,F,E四点是否共面为什么
答案
参考答案:
C,D,F,E四点共面.理由如下:
由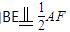 ,G是FA的中点知,
,G是FA的中点知,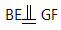 ,所以EF∥BG.
,所以EF∥BG.
由(1)知BG∥CH,所以EF∥CH,故EC,FH共面.又点D在直线FH上,所以C,D,F,E四点共面.
如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,
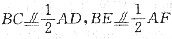 ,G,H分别为FA,FD的中点.
,G,H分别为FA,FD的中点.

C,D,F,E四点是否共面为什么
参考答案:
C,D,F,E四点共面.理由如下:
由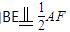 ,G是FA的中点知,
,G是FA的中点知,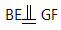 ,所以EF∥BG.
,所以EF∥BG.
由(1)知BG∥CH,所以EF∥CH,故EC,FH共面.又点D在直线FH上,所以C,D,F,E四点共面.