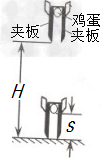
某兴趣小组研究在高空下落鸡蛋。若鸡蛋直接撞击地面，鸡蛋不被摔坏的最大高度为0.18m。如图所示，设计了一个保护鸡蛋的装置，用A、B两块较粗糙的夹板夹住鸡蛋，当鸡蛋离夹板下端某个距离时，多次实验发现，若将该装置从距地面H=4.5m高处从静止开始下落，鸡蛋恰好没有被摔坏，且鸡蛋整个下落时间为1.2s。设鸡蛋、夹板所受的空气阻力都为自身重力的0.1倍，装置碰地后速度立即变为零且保持竖直方向，不计装置与地面作用时间。取g=10m/s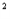。则

（1）没有装置保护，鸡蛋不被摔坏时鸡蛋着地的最大速度；

（2）夹板与鸡蛋之间的摩擦力是鸡蛋重力的几倍；

（3）当装置从H=4.5m高处下落，为了让鸡蛋能够落到地面，则鸡蛋在夹板中下落的最长距离s。