问题
计算题
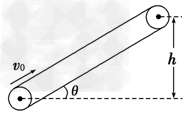
如图所示，绷紧的传送带与水平面的夹角θ＝30°，皮带在电动机的带动下，始终保持v0＝2 m/s的速率运行。现把一质量为m＝10 kg的工件(可视为质点)轻轻放在皮带的底端，经时间1.9 s，工件被传送到h＝1.5 m的高处，取g＝10 m/s2。求：
(1)工件与皮带间的动摩擦因数；
(2)工件相对传送带运动的位移。
答案
解：(1)由题意得，皮带长为：L＝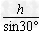
＝3 m
工件速度达到v0之前，从静止开始做匀加速运动，设匀加速运动的时间为t1，位移为s1，有：s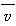1＝
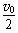t1＝
t1
设工件最终获得了与传送带相同的速度，则达到v0之后工件将做匀速运动，有：L－s1＝v0(t－t1)
解得：t1＝0.8 s<1.9 s，故假设工件最终获得与传送带相同的速度正确
加速运动阶段的加速度为：a＝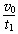
＝2.5 m/s2
在加速运动阶段，根据牛顿第二定律，有：μmgcosθ－mgsinθ＝ma
解得：μ＝0.866
(2)在时间t1内，传送带运动的位移为：s＝v0t1＝1.6 m
s1＝
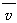t1＝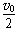
t1＝0.8 m
所以工件相对传送带的位移为：△s＝s－s1＝0.8 m