问题
计算题
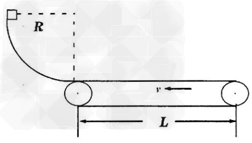
如图所示，一个可视为质点的物块，质量为m=2kg，从光滑四分之一圆弧轨道顶端由静止滑下，到达底端时恰好进入与圆弧轨道底端相切的水平传送带，传送带由一电动机驱动着匀速向左转动，速度大小为v=3m/s。已知圆弧轨道半径R=0.8m，皮带轮的半径r=0.2m，物块与传送带间的动摩擦因数为μ=0.1，两皮带轮之间的距离为L=6m，重力加速度g=10m/s2。求：
(1)皮带轮转动的角速度多大？
(2)物块滑到圆弧轨道底端时对轨道的作用力；
(3)物块将从传送带的哪一端离开传送带？物块，在传送带上克服摩擦力所做的功为多大？
答案
解：（1）皮带轮转动的角速度，由u=ωr，得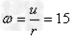
rad/s
（2）物块滑到圆弧轨道底端的过程中，由动能定理得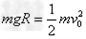
解得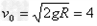
m/s
在圆弧轨道底端，由牛顿第二定律得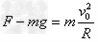
解得物块所受支持力F=60N
由牛顿第三定律，物块对轨道的作用力大小为60N，方向竖直向下
（3）物块滑上传送带后做匀减速直线运动，设加速度大小为a，由牛顿第二定律得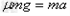 
解得a=1m/s2
物块匀减速到速度为零时向右运动的最大距离为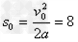
m>L=6m
可见，物块将从传送带的右端离开传送带
物块在传送带上克服摩擦力所做的功为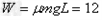
J