问题
问答题
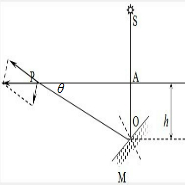
如图所示,折射率为n=
的液面上有一点光源S,发出一条光线,垂直地射到水平放置于液体中且距液面高度为h的平面镜M的O点上,当平面镜绕垂直于纸面的轴O以角速度ω逆时针方向匀速转动时,液面上的观察者跟踪观察,发现液面上有一光斑掠过,且光斑到P点后立即消失,求:2
(1)光斑在AP过程中的平均速度.
(2)光斑在P点即将消失时的瞬时速度.
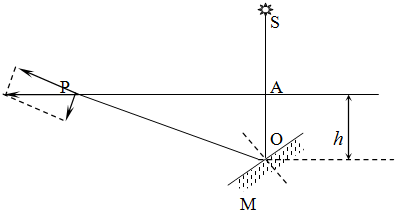
答案
根据折射定律:
=sinθ sin90°
=1 n 1 2
所以有:sinθ=
,2 2
解得:θ=45°
(1)因为θ=45°,则有:PA=OA=h,则镜面转过的角度为
,需要的时间为:t=π 8
=π 8 ω
,π 8ω
则镜面转动的平均速度为:
=. v
=h π 8ω
.8ωh π
(2)光斑转到P位置的速度是由光线的伸长速度和光线的绕O转动的线速度合成的,
光斑在P位置的线速度为2
h,2
所以光斑沿液面向左的速度为:v=
=4ωhv线 cos45°
答:(1)光斑在AP过程中的平均速度为
.8ωh π
(2)光斑在P点即将消失时的瞬时速度为4ωh.