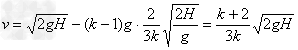问题
计算题
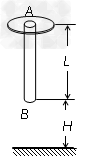
如图所示 ，厚度可不计的圆环套在粗细均匀的圆柱棒上端．圆环和圆柱棒质量分别为2m和m，圆环可在棒上滑动，它们之间滑动摩擦力和最大静摩擦力相等，大小为2kmg（k为大于1的常数）．棒能沿光滑的竖直细杆AB上下滑动．设棒与地相碰时无机械能的损失且碰撞时间极短．已知棒自由下落时下端距地面距离为H，与地经过多次碰撞后圆环才从棒的下端滑脱．求出第一次碰地后第二次碰地前环沿棒的相对滑动停止瞬间棒速度大小．
下面是一位同学的解法，如认为正确，说明理由；如认为不正确，指出错误并写出正确的解法．
解：第一次碰地瞬间的速度为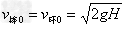
，方向向下 ①
第一次碰地后瞬间，依题意知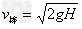
， 方向向上 ②
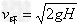，方向向下 ③
之后当两者停止相对滑动时，设共同速度为v，取向下为正方向，由动量守恒定律，得：
④
得：
．
答案
解：该同学的解法中的④式错误，因在第一次碰地后两者相对静止的过程中，环与棒系统有向下的重力，合外力不为零，故动量不守恒
正确解法为：接原解的③式：之后棒的加速度：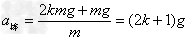
，方向向下
环的加速度：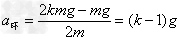
，方向向上
取向下方向为正方向，时间为t，有：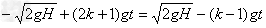
解得：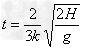
故相对静止的速度为：