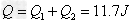问题
计算题
如图所示，质量为m=0.9kg的物块无初速的轻放在皮带传送带的A端。皮带以速度v=5m/s匀速运动。在距A端水平距离为3m处有一被细线悬挂的小球，刚好与皮带接触。细线长L=1.62m，小球的质量M=0.1kg。已知皮带足够长，μ=0.5，（g 取10m/s2）求：
(1)物块与球碰撞前物体的速度。
(2)若与球发生碰撞过程无机械能损失，则球能否完成圆周运动？若能，球到最高点时，计算出细线的拉力大小。
(3)物块从A端运动到B端由于相对滑动所产生的热量（设通过对球进行控制，球与物体没有再次相碰）。
答案
解：（1）物块轻放在匀速运动的皮带上即在滑动摩擦力作用下做加速运动，由牛顿第二定律：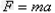
可得加速度：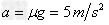
由运动学公式：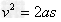
，可知
时，达到与皮带相同的速度，即开始做匀速运动，所以物块与球碰撞前物体的速度为5m/s
（2）由于碰撞过程无机械能损失，碰撞过程中动量和动能均守恒
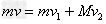
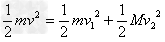
联立解得：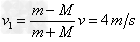
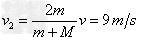
设被细线悬挂的小球能做圆周运动到最高点，到达的速度为
，此时细线的拉力为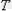
。运动中只有重力做功，故小球的机械能守恒
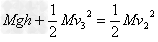
其中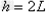
，代入数据，求得
小球在最高点时，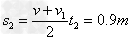
代入数据，求得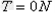
（3）物块在A端从静止开始加速到5m/s，加速运动的时间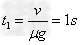
，此时物块和皮带的位移分别为2.5m和5m
故在第一次运动过程中由于相对滑动所产生的热量为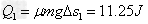
物块与小球碰撞后继续运动到再次与皮带相对静止，经历的时间为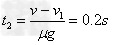
此过程中物块的位移为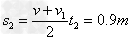；皮带的位移为1m
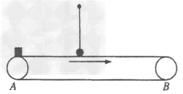
故在第二次运动过程中由于相对滑动所产生的热量为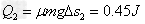
∴