问题
问答题
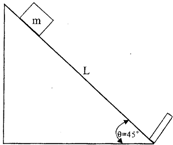
一固定的斜面,倾角为45°,斜面长L=2.0米,在斜面下端有-与斜面垂直的挡板.一质量为m的滑块,从斜面的最高点沿斜面下滑,初速度为零.滑块沿斜面下滑到斜面最低端与挡板发生弹性碰撞(碰撞前后能量没有损失).已知滑块与斜面间的滑动摩擦系数μ=0.2.试求:
(1)滑块与挡板发生第1次碰撞时的速度大小及反弹后上升的最大距离?
(2)此滑块从开始运动到与挡板发生第5次碰撞前的过程中运动的总路程.
答案
(1)由动能定理得mgLsinθ-fL=
mv12-0①1 2
且f=μmgcosθ ②
由①②得
v1=
=2gL(sinθ-μcosθ)
m/s=4.8m/s2×10×2(
-0.2×2 2
)2 2
滑块向上运动由动能定理得-mgL1sinθ-fL1=0-
mv12 ③1 2
由方程①②③得
=L1 L
=sinθ-μcosθ sinθ+μcosθ 2 3
所以反弹后上升的最大距离为
×2=1.33m2 3
(2)令α=
=L1 L
,则L1=αL2 3
同理第2次碰撞后上升的距离为L2=αL1=α2L
第3次碰撞后上升的距离为L3=αL2=α3L
…
第1次碰撞前通过的路程s1=L
第2次碰撞前通过的路程s2=L+2L1=L+2αL
第3次碰撞前通过的路程s3=L+2L1+2L2=L+2αL+2α2L
…
第5次碰撞前通过的路程S5=L+2αL+2α2L+2α3L+2α4L=L(1+2α(
))α4-1 α-1
代入数值得s5=8.42 m
答:(1)滑块与挡板发生第1次碰撞时的速度大小为4.8m/s,反弹后上升的最大距离为1.33m;
(2)此滑块从开始运动到与挡板发生第5次碰撞前的过程中运动的总路程为8.42m.
