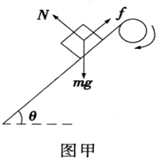
（1、2）对放在传送带上的小物体进行受力分析，

小物体沿传送带向下滑动时，无论传送带时静止还是沿顺时针分析正常转动，小物体的受力情况完全一样，

都是在垂直传送带的方向受力平衡，受到沿传送带向上的滑动摩擦力，

如图甲所示，

根据牛顿第二定律，小物体沿传送带下滑的加速度为：

a₁=

mgsinθ-μmgcosθ

m

=g（sinθ-μcosθ）=10×（0.6-0.5×0.8）m/s²=2m/s²，

小物体从A端运动到B端做初速度为零的匀加速直线运动，设需要的时间为t，则

s=

1

2

a₁t²，

t=

2s a1

=

2×16 2

s=4s

（3）当传送带沿逆时针方向正常转动时，开始时，传送带作用于小物体的摩擦力沿传送带向下，

小物体下滑的加速度a₂=g（sinθ+μcosθ）=10m/s²

小物体加速到与传送带运行速度相同是需要的时间为

t₁=

v

a2

=

10

10

s=1s，

在这段时间内，小物体沿传送带下滑的距离为s₁=

1

2

at²=

1

2

×10×1=5m

由于 μ＜tanθ，

此后，小物体沿传送带继续加速下滑时，它相对于传送带的运动的方向向下，

因此传送带对小物体的摩擦力方向有改为沿传送带向上，

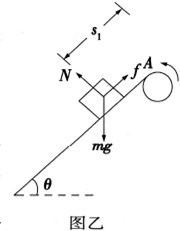
如图乙所示，

其加速度变为a₁=g（sinθ-μcosθ）=10×（0.6-0.5×0.8）m/s²=2m/s²

小物体从该位置起运动到B端的位移为s-s₁=16m-5m=11m

小物体做初速度为v=10m/s、加速度为a₁的匀加速直线运动，

由s-s₁=vt₂-

1

2

a₁t₂²

代入数据，解得t₂=1s（t₂=-11s舍去）

所以，小物体从A端运动到B端的时间为t=t₁+t₂=2s．

答：（1）如果传送带停止运行，小物体从A端运动到B端的时间为4s；

（2）如果传送带沿顺时针方向正常转动，小物体从A端运动到B端的时间为4s；

（3）如果传送带沿逆时针方向正常转动，小物体从A端运动到B端的时间为2s．