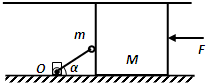
如图所示,高为0.3m的水平通道内,有一个与之等高的质量为M=1.2kg表面光滑的立方体,长为L=0.2m的轻杆下端用铰链连接于O点,O点固定在水平地面上竖直挡板的底部(挡板的宽度可忽略),轻杆的上端连着质量为m=0.3kg的小球,小球靠在立方体左侧.取g=10m/s2,sin37°=0.6,cos37°=0.8.
(1)为了使轻杆与水平地面夹角α=37°时立方体平衡,作用在立方体上的水平推力F1应为多大?
(2)若立方体在F2=4.5N的水平推力作用下从上述位置由静止开始向左运动,则刚要与挡板相碰时其速度多大?
(3)立方体碰到挡板后即停止运动,而轻杆带着小球向左倒下碰地后反弹恰好能回到竖直位置,若小球与地面接触的时间为t=0.05s,则小球对地面的平均冲击力为多大?
(4)当杆回到竖直位置时撤去F2,杆将靠在立方体左侧渐渐向右倒下,最终立方体在通道内的运动速度多大?
(1)对小球有N=
=mg tan37°
N=4N0.3×10 3 4
F=N=4N
(2)FLcos37°-mg(L-Lsin37°)=
(m+M)v121 2
可解得:v1=0.8m/s
(3)设小球碰地的速度为v2,有 mgL+
mv12=1 2
mv221 2
可解得 v2=2.15m/s
设小球碰地后反弹的速度为v3 有
mv32=mgL 1 2
可解得 v3=2m/s
对小球的碰地过程,根据牛顿第二定律有 (N-mg)=m v3+v2 t
可解得 N=27.9N
(4)设杆靠在立方体向右倒下与地面的夹角为θ时小球与立方体分离,此时小球与立方体的速度分别为v4和v5,可有
mgL(1-sinθ)=
mv4 2+1 2
Mv5 21 2
v4sinθ=v5
mgsinθ=mv42 L
联立上述方程可解得 v5=0.5m/s.
答:(1)为了使轻杆与水平地面夹角α=37°时立方体平衡,作用在立方体上的水平推力F1应为4N;
(2)若立方体在F2=4.5N的水平推力作用下从上述位置由静止开始向左运动,则刚要与挡板相碰时其速度0.8m/s;
(3)小球对地面的平均冲击力为27.9N;
(4)最终立方体在通道内的运动速度为0.5m/s.
