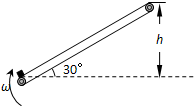
如图所示,电动机带着绷紧的传送皮带始终以υ0=2m/s的速度运动,传送带与水平面的夹角为30°,现把某一工件轻轻地放在皮带的底端,经过一段时间后,工件被送到高h=2m的平台上,在此过程中电动机由于传送工件多消耗的电能为420J.已知工件与皮带间的动摩擦因数μ=
,除此之外,不计其他损耗,g=10m/s2,求:(1)工件从传送皮带底端运动到顶端所用的时间;(2)此工件的质量为多少.3 2
(1)工件刚开始运动时与传送皮带之间有相对滑动,
工件刚开始沿传送皮带向上匀加速运动.
斜面长度L=
=4m;h sin30°
工件匀加速运动时,由牛顿第二定律得:
μmgcos30°-mgsin30°=ma,
解得:工件的加速度a=μgcos30°-gsin30°=2.5m/s2,
工件达到速度υ0=2m/s,所需时间t1=
=0.8s,v0 a
此过程工件沿传送皮带向上运动的位移x1=
at12=0.8m<L,1 2
在此之后由于工件与传送皮带相对静止,工件以υ0=2m/s的速度匀速直线运动
工件匀速运动经历t2=
=1.6s,L-x1 v0
工件从传送皮带底端运动到顶端所用的时间t=t1+t2=2.4s.
(2)在工件匀加速运动过程中传送皮带运动的距离为x2=v0t1=1.6m,
此过程中的相对位移为△x=x2-x1=0.8m,
电动机由于传送工件多消耗的电能为:
△E=μmgcos30°△x+
mv02+mgh,1 2
由以上各式可得m=15kg;
答:(1)工件从传送皮带底端运动到顶端所用的时间2.4s;(2)此工件的质量为15kg.

