问题
填空题
在梯形ABCD中,AB∥CD,AC、BD相交于点O,若AC=5,BD=12,中位线长为
|
答案
作BE∥AC,
∵AB∥CE,∴CE=AB,
∵梯形中位线为6.5,
∴AB+CD=13,
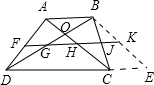
∴DE=CE+CD=AB+CD=13,
∵BE=AC=5,BD=12,由勾股定理的逆定理,
得△BDE为直角三角形,即∠EBD=∠COD=90°,
设S△EBD=S
则S2:S=DO2:DB2
S1:S=OB2:BD2
∴
+S1
=S2 S
∵S=12×5×
=301 2
∴
+S1
=S2
.30
故本题答案为:
.30
