问题
问答题
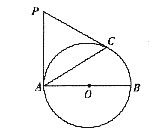
如图,已知AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,∠BAC=30°.
(1)求∠P的大小;
(2)若AB=2,求PA的长(结果保留根号).
答案
参考答案:
(1)因为PA是⊙O的切线,AB为⊙O的直径,
所以PA⊥AB,
所以∠BAP=90°.
因为∠BAC=30°,
所以∠CAP一90°-∠BAC=60°.
又因为PA、PC切⊙O于点A、C,
所以PA=PC,
所以△PAC为等边三角形,
所以∠P=60°.
(2)如图,连接BC,
则∠ACB=90°.
在Rt△ACB中,AB=2,∠BAC=30°,
所以AC=AB·cos∠BAC=2cos30°=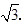
因为△PAC为等边三角形PA=AC,
所以PA=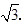 ;
;
