问题
问答题
一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同)，其中有白球2个，黄球1个，若从中任意摸出一个球，这个球是白球的概率为0.5．
(1)求口袋中红球的个数；
(2)若从中摸出一个球后不放回，再摸出一个球，通过画树状图或列表分析，求两次均摸到白球的概率．
答案
参考答案：
设红球的个数为x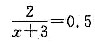
，解得x=1．
经检验：x=1是所列方程根且符合题意．
答：口袋中红球的个数为1个．
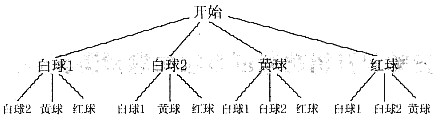
(2)用树状图分析如下：
或列表分析：
| 白球1 | 白球2 | 黄球 | 红球 | |
| 白球1 | (白2，白1) | (黄，白1) | (红，白1) | |
| 白球2 | (白1，白2) | (黄，白2) | (红，白2) | |
| 黄球 | (白1，黄) | (白2，黄) | (红，黄) | |
| 红球 | (白1，红) | (白2，红)， | (黄，红) |
共有12种可能结果，其中2个白球的可能结果是2个．
所以两次均摸到白球的概率为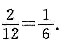
答：两次均摸到白球的概率为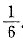
.