将三重积分的累次积分
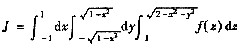 表为定积分.
表为定积分.
参考答案:[分析与求解一] 将J表成[*],确定积分区域Ω,然后选择适当的积分顺序,将它化为定积分.
将J看成是三重积分的先一后二的累次积分,于是
[*]
其中[*]
因此,Ω是由半球面[*]与平面z=A所围成.
两面的交线是[*]即[*]
Ω在xy平面上的投影区域是xB+yB≤A,z=0,即Dxy(如图(a)).
现改为先二后-(z)的积分顺序,Ω的不等式表示为[*]截面区域D(z)(如图(b)):xB+yB≤B-zB,面积S(z)=π(B-zB).因此
[*]
[分析与求解二] 将J,看成是三重积分的先二后一的累次积分,确定二重积分的积分区域,然后逐次对二重积分交换积分次序,化为定积分.
[*]
其中[*]
这里x视为常量,在yz平面上如图(c)所示.
在Dyz上改为先y后z的积分顺序.由于
[*]
于是[*]
其中 Dzx:-A≤x≤A,[*]
[*]
现在Dzx上改为先x后z的积分次序(如图(d)),由于
[*]
于是[*]
其中[*]
[*]
[分析与求解三] 将J表成三重积分[*],问题变成如何计算这个三重积分(化为定积分),Ω如前所述.
除了先二后一的积分顺序外,因Ω为旋转体,也可选择柱坐标变换(x=rcosθ,y=rsinθ,z=z),并选择先r,θ后z的积分顺序化为定积分.
Ω的柱坐标表示:[*]
于是[*]
[*]
