问题
填空题
设y=f(x)二阶可导，f’(x)≠0，它的反函数是x=ψ(y)，又f(0)=1，
f"(0)=-1，则
______.
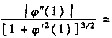答案
参考答案：[*]
解析：[分析一] 由反函数求导公式得
[*]
再由复合函数求导法得
[*]
从而[*]
于是[*]
[分析二] 将上述导出的ψ’(γ)，ψ"(γ)表达式代入得
[*]
于是[*]
[分析三] 在xOy直角坐标系中y=f(x)与它的反函数x=ψ(y)代表同一条曲线，作为x的函数y=f(x)与作为y的函数x=ψ(y)在同一点处的曲率是相同的，按曲率公式应有
[*]
[*]
因f(0)=1，即x=0时[*]
[*]
