设f(x)是(-∞,+∞)上以T为周期的周期函数,且
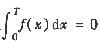 .此外又存在常数L>0使得对任何x,y∈(-∞,+∞)有|f(x)-f(y)|≤L|x-y|.求证:
.此外又存在常数L>0使得对任何x,y∈(-∞,+∞)有|f(x)-f(y)|≤L|x-y|.求证:
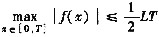 .
.
参考答案:由[*]x,y∈(-∞,+∞)有|f(x)-f(y))|≤L|x-y|可知f(x)是(-∞,+∞)上的连续函数,从而存在xM∈[0,T]使得
[*]
由连续函数的积分中值定理可知,存在x0∈(0,T)使得
[*]
以下分情况讨论:
①当xM=x0时,这时有|f(xM)|=|f(x0)|=0,即f(x)=0在[0,T]上成立,由f(x)的周期性即知f(x)≡0在(-∞,+∞)上成立,故[*],从而结论显然成立.
②当xM>x0时,由f(x)的周期性可得
2|f(x0)-f(xM)|=|f(x0)-f(xM)|+|f(x0)-f(xM)|
=|f(x0)-f(xM)|+|f(x0+T)-f(xM)|
≤L(xM-x0)+L(x0+T-xM)=LT,
即此时要证明的不等式|f(xM)|=|f(x0)-f(xM)|≤[*]LT成立.
③当xM<x0时,仍然由f(x)的周期性可得
2|f(x0)-f(xM)|=|f(xM)-f(x0)|+|f(xM)-f(x0)|
=|f(xM)-f(x0)|+|f(xM+T)-f(x0)|
≤L(x0-xM)+L(xM+T-x0)=LT,
即此时要证明的不等式|f(xM)|=f(x0)-f(xM)|≤[*]LT也成立.
综合以上讨论即知在题设条件下总有[*]成立.
