问题
填空题
设二元函数f(u，v)具有二阶连续偏导数，且满足
，又g(x，y)=f(x2-y2，2xy)，则
=______．
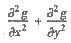答案
参考答案：0
解析：
[分析]： 直接计算可得
dg=f’ud(x2-y2)+f’vd(2xy)=f’u·(2xdx-2ydy)+f’v·(2ydx+2xdy)
=(2xf’u+2yf’v)dx+(-2yf’u+2xf’v)dy，
从而 g’x=2xf’u+2yf’v， g’y=-2yf’u+2xf’v．
继续求偏导数又可得
g"xx=2f’u+2x(f’u)’x+2y(f’v)’x=2f’u+2x(2xf"uu+2yf"iv)+2y(2xf"vu+2yf"vv)
=2f’u+4x2f"uu+8xyf"uv+4y2f"vv，
g"yy=-2f’u-2y(-2rf"uv+2xf"v)+2x(-2yf"vu+2xf"vv)
=-2f’u+4y2f"uu-8xg"uv+4x2f"vv．
由止E即得g"xx+g"yy=4(x2+y2)(f"uu+f"vv)=0．