问题
解答题
某商场将进价为30元的书包以40元售出， 平均每月能售出600个，调查表明：这种书包的售价每上涨1元，其销售量就减少10个。
（1）请写出每月售出书包的利润y元与每个书包涨价x元间的函数关系式；
（2）设每月的利润为10000的利润是否为该月最大利润？如果是，请说明理由；如果不是，请求出最大利润，并指出此时书包的售价应定为多少元。
（3）请分析并回答售价在什么范围内商家就可获得利润。
答案
略
分析：（1）根据设每个书包涨价x元，由这种书包的售价每上涨1元，其销售量就减少10个，列出函数关系式，
（2）用配方法求出二次函数的最大值即可，
（3）令二次函数等于0，利用二次函数的性质解得x的取值范围．
解答：解：（1）∵每个书包涨价x元，
∴y=（40-30+x）（600-10x），
=-10x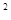
+500x+6000，
答：y与x的函数关系式为：y=-10x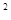+500x+6000；
（2）∵y=-10x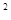+500x+6000=-10（x-25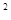）+12250，
∴当x=25时，y 有最大值12250，
即当书包售价为65元时，月最大利润为12250元，10000元不是月最大利润；
（3）解方程-10x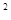+500x+6000="0"
得，x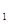
=60，x
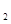=-10，
即当涨价60元时和降价10元时利润y 的值为0，
由该二次函数的图象性质可知，
当涨价大于60元时以及降价超过10元时利润y 的值为负，
所以书包售价在大于30元且低于100元时商场就有利润．
点评：此题主要考查了二次函数的应用，准确分析题意，列出y与x之间的二次函数关系式是解题关键．