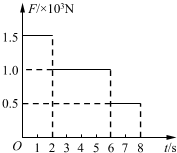
竖直运行的升降机地板上有一个质量为100kg的物体,它对地板的压力随时间变化的图象如图所示.若升降机从静止开始向上运动,g取10m/s2,求8s内升降机上升的高度?
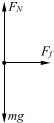
取升降机地板上的物体为研究对象,物体受力情况如右图所示.取向上为正方向.由牛顿第三定律可知,物体对地面的压力等于地面对物体的支持力,即F=FN.
在0~2s内,FN1=F1>mg,物体所受合外力竖直向上,所以物体向上做匀加速直线运动.
由牛顿第二定律得 FN1-mg=ma1①
a1=
=FN1-mg m
m/s2=5.0m/s21.5×103-100×10 100
所以物体的位移 x1=
a11 2
=t 21
×5.0×2.02m=10.0m②1 2
物体2s末的速度 v=a1t1=5.0×2.0m/s=10.0m/s③
在2~6s内,FN2=mg,物体所受合外力为零,所以物体向上做匀速直线运动,则
物体的位移 x2=vt2=10.0×4.0m=40.0m④
在6~8s内,FN3<mg,物体所受合外力方向竖直向下,所以物体向上做匀减速直线运动,初速度为v=10.0m/s.
由牛顿第二定律F3-mg=ma3⑤
a3=
=F3-mg m
m/s2=-5.0m/s2500-100×10 100
所以物体的位移 x3=vt3+
a31 2
=10.0×2m+t 23
×(-5.0)×2.02m=10.0m⑥1 2
所整个过程中物体位移x=x1+x2+x3=10.0m+40.0m+10.0m=60.0m⑦
答:8s内升降机上升的高度为60.0m.
