问题
问答题
设f(t),g(t)与y(t)均为[a,b]上的连续函数,f(t)>0且

试证明在[a,b]上成立不等式:
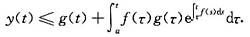
答案
参考答案:令[*]
有y(t)-g(t)≤R(t)
又R’(t)=f(t)y(t)≤f(t)g(t)+f(t)R(t),进一步有
R’(t)-f(t)R(t)≤f(t)g(t),
[*]
即[*]
上式两边在[a,t]上积分,并注意到R(a)=0,有
[*]
