问题
问答题
设
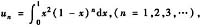讨论级数
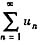的敛散性，当此级数收敛时，试求其和。
答案
参考答案：[解法一] 首先用换元积分法求un的值，令1-x=t，于是x=1-t，且x:0→1[*]t:1→0，dx=-dt，代入即得
[*]
故[*]
其次，用定义讨论它的敛散性，因为
[*]
故 Sn=u1+u2+…+un
[*]
由此可见[*]这表明级数[*]收敛，且其和为[*]
[解法二] 用分部积分法求un的值，即
[*]
由于[*]且级数[*]收敛，因此，根据正项级数的比较判别法知级数[*]收敛，注意
[*]
于是[*]的前n项部分和
Sn=u1+u2+…+un
[*]
故[*]