计算二重积分
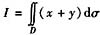 ,其中积分区域D是由曲线
,其中积分区域D是由曲线
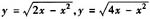 以及直线x=2围成。
以及直线x=2围成。
参考答案:[解法一] 积分区域D可表示为[*]如图,则有
[*]
[*]
而[*]
代入即得所求二重积分
[*]
[解法二] 为简化计算将积分区域D表示为D=D1\D2,其中D1是上半圆域(x-2)2+y2≤4且y≥0中横坐标满足0≤x≤2的四分之一圆域,即D1={(x,y)|0≤x≤2,0≤y≤[*],D2是上半圆域(z-1)2+y2≤1且y≥0,即D2={(x,y)|0≤x≤2,0≤y≤[*]从而
[*]
为了计算二重积分I1,I2简便起见,可分别在D1与D2上作适当的平移变换,而后再作极坐标变换。
对于I1,令u=x-2,v=y[*]x=u+2,Y=v,则D1变成
D’1={(u,v)|v2+v2≤4,v≥0,-2≤u≤0},
令u=rcosθ,v=rsinθ,在极坐标系(r,θ)中[*]故
[*]
对于I2,令u=x-1,v=y[*]x=u+1,y=v,则D2变成
D’2={(u,v)u2+v2≤1,v≥0},
令u=rcosθ,v=rsinθ,在极坐标系(r,θ)中D’2={(r,θ)|0≤θ≤π,0≤r≤1