问题
填空题
已知函数y＝Asin(ωx＋φ)＋m(A>0，ω>0，|φ|<)的最大值为4，最小值为0，最小正周期为，直线x＝是其图象的一条对称轴，则符合条件的函数解析式是
答案
y＝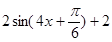
由题意可得A+m=4，A-m=0，解得 A=2，m=2．
再由最小正周期为，可得
=，解得ω=4，
∴函数y=Asin（ωx+φ）+m=2sin（4x+φ）+2．
再由 x=是其图象的一条对称轴，可得 4×+φ=kπ+，k∈z，又|φ|＜，
∴φ=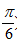
，
故符合条件的函数解析式是 y=2sin（4x+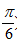）+2，
故答案为 y=2sin（4x+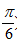）+2