问题
解答题
(本题9分)
已知函数f(x)=2cosx(sinx-cosx)+1。
(1)求函数f(x)的最小值以及取最小值时x的取值;
(2)求函数f(x)的单调递增区间。
答案
解:f(x)=2cosx·sinx-2cos2x+1=sin2x-cos2x=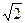 sin(2x-
sin(2x-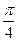 )
)
(1)f(x)min=-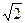 ,2x-
,2x-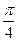 =2k
=2k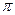 -
-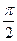 ,x=k
,x=k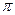 -
-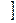 . (k
. (k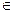 Z)
Z)
(2)2k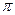 -
-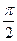 ≤2x
≤2x -
-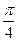 ≤2k
≤2k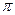 +
+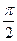 , k
, k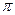 -
-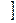 ≤x≤k
≤x≤k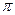 +
+ .(
.( k
k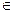 Z)
Z)
∴单调增区间为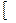 k
k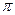 -
-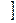 , k
, k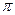 +
+
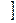 .(k
.(k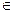 Z)
Z)
