有一边长为a，密度为ρ的立方体大理石，工人用一根粗细均匀的单

问题问答题

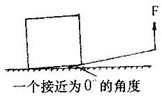
有一边长为a，密度为ρ的立方体大理石，工人用一根粗细均匀的单位长度重为P牛的铁棒将石块撬起一个很小的角度．如图所示，如果插入的长度为石块边长的四分之一，并保持该长度不变，则当选用的铁棒多长时，向上施加的力最小？此最小的力多大？

答案

由题意可知，物体的重力为G=mg=ρa³g；

设铁棒长为L，动力为F．由题可知铁棒的重力提供的阻力，作用点在铁棒的重心上，阻力臂为

L；因重物箱的密度均匀且铁棒插入的长度为箱宽的四分之一，则重物的一半重力提供阻力，阻力臂为

a；力F提供动力，动力臂为L．由杠杆的平衡条件得：F₁L₁=F₂L_{2
即：
1
4
a?1
2ρa³g+LP?1
2L=FL
解得人对杠杆的力：
F=
ρa4g
8
+pL2
2
L
=ρa4g
8L+p
2
L
由数学知识a²+b²≥2ab，当a=b时取最小值，可得
当=
ρa4g
8L
=p
2
L时，即L=a2
2
ρg
p时F有最小值．
F的最小值为：F=
a2
2
ρgP
．
答：当选用的铁棒长度为L=
a2
2
ρg
p
时，施加的力最小；这个最小的力是F=a2
2
ρgP．}