问题
计算题
（10分）一质量为m ="40" kg的小孩站在电梯内的体重计上.电梯从t =0时刻由静止开始上升,在0到6 s内体重计示数F的变化如图所示.试问：在这段时间内电梯上升的高度是多少？取重力加速度g="10" m/s2.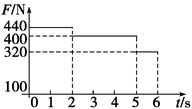
答案
9（m）
题目分析：选取小孩为研究对象，地面为参考系，小孩受到重力和体重计对小孩的弹力，如图所示.小孩的运动分为三个阶段.在0~2s内以加速度a1向上做匀加速直线运动，根据牛顿第二定律可得，加速度
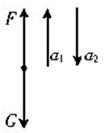
a1=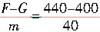
=1（m/s2）
根据匀变速直线运动公式可得，第一阶段位移s1=1/2a1t12=1/2×1×22=2（m）
第一阶段末速度
v1=a1t1=1×2=2（m/s）
2s~5s内向上以速度v1做匀速直线运动，根据匀速直线运动公式可得，第二阶段位移
s2=v1t2=2×3=6（m）
在5s~6s内以加速度a2向上做匀减速直线运动，根据牛顿第二定律可得，加速度
a2=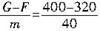
=2（m/s2）
设从速度v1减速为0的时间为t3，根据匀变速直线运动公式可得t3=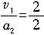
=1（s）
则可判断小孩子在第6s末速度为0，第三阶段位移
s3=v1t3-1/2a2t32=2×1-1/2×2×12=1（m）
则在这段时间内小孩上升的高度，即电梯上升的高度
s=s1+s2+s3=2+6+1=9（m）
点评：难度中等，本题为多过程问题，注意把整个过程分解为独立分析的分过程，联系分过程的桥梁就是速度，结合牛顿第二定律和运动学公式求解