问题
计算题
两束平行的细激光束，垂直于半圆柱玻璃的平面射到半圆柱玻璃上，如图甲所示。已知其中一条光线沿直线穿过玻璃，它的入射点是O；另一条光线的入射点为A，穿过玻璃后两条光线交于P点。已知玻璃截面的圆半径为R，OA=
，OP =
R。求：
（1）该种玻璃材料的折射率。
（2）若使用该种材料制作成如图乙所示的扇形透明柱状介质AOB，半径为仍R，圆心角
。一束平行于OB的单色光由OA面射入介质，要使柱体AB面上没有光线射出，至少要在O点竖直放置多高的遮光板？（不考虑OB面的反射）
答案
（1）=1.73（2）=R/3。
（1）作出光路如图所示，
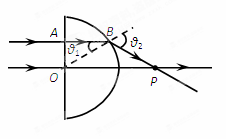
其中一条光线沿直线穿过玻璃，可知O点为圆心；
另一条光线沿直线进入玻璃，在半圆面上的入射点为B，入射角设为θ1，折射角设为θ2
则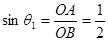
得θ1=300
因OP=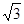
R，由几何关系知BP=R，则折射角θ2=600
由折射定律得玻璃的折射率为
n=
=1.73
（2）光线在OA面上的C点发生折射，入射角为60°，折射角为β，
n=sin60°/sinβ，
解得β=30°。
折射光线射向球面AB，在D点恰好发生全反射，入射角为α，
n=1/sinα，
sinα=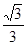
> sin30°.
在三角形OCD中，由正弦定理，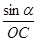
=
，
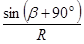挡板高度H=OCsin30°=R/3。