参考答案：

解析：我们称符合下列特征的 * * 为公平赌博：令R为该 * * 的随机净收益(随机现金流入扣除现金流出以后的差额)，有E(R)=0，Var(R)＞0。
根据对待公平 * * 的态度不同，我们可以将投资者划分为风险厌恶型投资者、风险喜好型投资者和风险中性投资者三大类。
令W为投资者在期初所拥有韵确定性财富，R为某公平赌博的随机净收益。如果EU(W+R)＜U(W)，则称该投资者为风险厌恶型投资者。可见，风险厌恶型投资者不喜欢公平赌博。
如果EU(W+R)＞U(W)，则称该投资者为风险喜好型投资者。可见，风险喜好型投资者喜欢公平赌博。
如果EU(W+R)=U(W)，则称该投资者为风险中性投资者。可见，风险中性投资者对公平赌博抱着无所谓的态度。
实际上，风险厌恶型投资者的效用函数为凹型的，满足U[E(R)]＞EU(R)，其中，R为某不确定性决策的随机后果向量，E(R)为该不确定性决策各种后果的期望值。
例如，假定某 * * 仅有两种可能的结果R₁和R₂，即R=(R₁，R₂)，则对于风险厌恶型投资者来说，有：U[aR₁+(1-a)R₂]＞aU(R₁)+(1-a)U(R₂)。其中，a∈(0，1)为可能结果R₁发生的概率，(1-a)为可能结果R₂发生的概率。
风险喜好型投资者的效用函数为凸型的，满足U[E(R)]＜EU(R)。
仍以上述有两种可能结果的 * * 为例，对于风险喜好型投资者来说，有：
U[aR₁+(1-a)R₂]＜aU(R₁)+(1-a)U(R₂)
风险中性投资者的效用函数为线性的，满足U[E(R)]=EU(R)。
以上述有两种可能结果的 * * 为例，对于风险中性投资者来说，有：
U[aR₁+(1-a)R₂]=aU(R₁)+(1-a)U(R₂)
三类投资者效用函数的几何形式如下图所示：

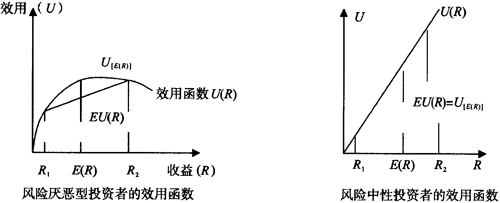
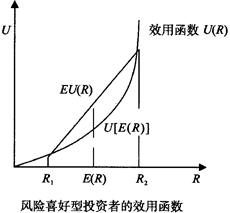
可见，风险厌恶型投资者的效用函数U=U(R)的一次导数大于零，二次导数小于零；风险喜好型投资者的效用函数U=U(R)的一次导数和二次导数均大于零；而风险中性投资者的效用函数U=U(R)的一次导数大于零，二次导数等于零。
就本题来说，已知该投资者的效用函数为U=0.5+R²，其一次导数

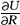=2R＞0，二次导数

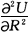=2＞0。可见，该投资者属于风险喜好类型的投资者。
(2)该投资者若将其10000元资本全部存入银行，则其年利息收入为10000×2%=200元。且这笔利息收入是确定的，毫无风险。相应的效用值为U[E(R)]=U(0.2)。(注意R的单位是千元)
该投资者若将其10000元资本全部投资于某种股票，则其年期望收益为E(R)8000×40%-5000×60%=200元。相应的效用值为：
EU(R)=U(8)×40%+U(-5)×60%
可见，若不考虑其他因素，即仅仅考虑这一年当中的投资收益，由于该投资者喜好风险，根据U[E(R)]＜EU(R)，所以其将会把所有资本全部投资于股票。
(3)若投资股票，他的效用是：
EU(R)=U(8)×40%+U(-5)×60%
=[0.5+8²]×40%+[0.5+(-5) ²]×60%
=41.4
存入银行的效用为U=(0.5)+(0.2) ²=0.54