问题
问答题
如果f(x)在[0,1]上二阶可导,且f(0)=f(1)=1,

试证:
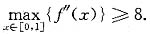
答案
参考答案:因为f(x)在[0,1]上二阶可导,所以在[0,1]上f’(x)存在且连续,进而知f(x)在[0,1]上连续,由题设知[*]我们令f(x0)=0,易见x0≠0,1,所以0<x0<1
由于f(x)在x0点可导且在x0点取最小值,所以f’(x0)=0
将f(x)按(x-x0)的幂展开为二阶泰勒公式,有
[*]
其中ξ在x与x0之间,考虑到f(x0)=f’(x0)=0,有
[*]
即
[*]
取x=0,1,并考虑到f(0)=f(1)=1,有
[*]
于是,当[*]时,有
[*]
当[*]时,有
[*]
从而,有
[*]
解析:
[分析]: 欲证的结论中含有f"(x),这使人想到泰勒公式.进一步考虑,应将f(x)展成哪一点处的二阶泰勒公式呢显然该点应该是函数f(x)的零点。
