问题
计算题
如图所示，传送带与水平地面夹角为θ=37°，以10m/s的速度转动，在传送带上端轻轻地放一个质量m=0.5㎏的物体，它与传送带间的动摩擦因数μ=0.5，已知传送带从A到B的长度L=44m，则物体从A到B需要的时间为多少？（sin37°=0.6，cos37°=0.8,g取10m/s2）
答案
4s或者 t＝
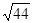s
题目分析：（1）当传送带逆时针转动时，物体放在传送带上后，开始阶段物体受力情况如图甲所示，
由沿斜面方向：mgsinθ+Ff=ma
垂直于斜面方向 FN -mgcosθ＝0
又Ff=μFN，得mgsinθ＋μmgcosθ＝ma1， a1＝10×(0.6＋0.5×0.8) m/s2＝10 m/s2
物体加速至与传送带速度相等需要的时间t1＝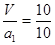
s＝1 s
t1时间内位移x＝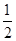
a1t12＝5 m
当物体速度大于传送带速度时，此物体受力情况如图14乙所示，
由沿斜面方向：mgsinθ-Ff=ma
垂直于斜面方向 FN -mgcosθ＝0
又Ff=μFN得mgsinθ－μmgcosθ＝ma2，得a2＝2 m/s2
设后一阶段物体滑至底端所用的时间为t2，由L－x＝vt2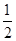＋a2t22解得t2＝3 s，t2＝－13 s(舍去)
所以物体由A→B的时间t＝t1＋t2＝4 s.
（2）当传送带顺时针转动时，物体放在传送带上后，开始阶段物体受力情况如图乙所示，
由沿斜面方向：mgsinθ-Ff=ma
垂直于斜面方向 N -mgcosθ＝0
又Ff=μＮ得 mgsinθ－μmgcosθ＝ma3得a2＝2 m/s2
x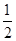＝a3t2＝44 m 解得 t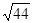＝s