问题
问答题
设
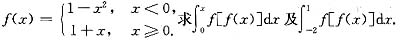
答案
参考答案:由复合函数的概念知,
当x<-1时,f(x)=1-x2<0,故
f[f(x)]=1-[f(x)]2=1-(1-x2)2=2x2-x4,
当-1≤x<0时,f(x)-1-x2≥0,故
f[f(x)]=1+f(x)=1+(1-x2)=2-x2,
当x≥0时,f(x)=1+x>0,故
f[f(x)]=1+f(x)=1+(1+x)=2+x,
综上有
[*]
于是,
当x<-1时,
[*]
当-1≤x<0时,
[*]
当x≥0时,
[*]
从而[*]

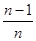 倍
倍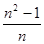 倍
倍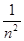 倍
倍