问题
问答题
曲线y=f(x)(x≥0，y≥0)连续且单调，从其上任一点A作x轴与y轴的垂线，垂足分别是B和C，若由直线AC，y轴和曲线本身包围的图形的面积等于矩形OBAC的面积的
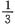，求曲线的方程。
答案
参考答案：(1) 如图3所示，当f(x)单调增加时，在曲线上任取点A(a，f(a))，由题意得
[*]
[*]
即：[*]
两边对a求导得
3f(a)=Bf(a)+2af’(a)
化简得[*]积分得[*]
于是所求曲线方程为[*](其中C为任意常数)。
(2) 如图4所示，当f(x)单调减少时，有
[*]
[*]
化简求导得：[*]积分得[*]
于是所求曲线方程为[*](C为任意常数)。