问题
填空题
设f(x)满足
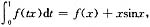f(0)=0且有一阶导数，则当x≠0时，f’(x)=______。
答案
参考答案：-2sinx-xcosx
解析：[详解] 令u=tx，则有[*]于是
[*]
即[*]
两边对x求导，f(x)=f(x)+xf’(x)+2xsinx+x2cosx，x≠0
故 f’(x)=-2sinx-xcosx
搜题请搜索小程序“爱下问搜题”
设f(x)满足
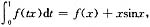f(0)=0且有一阶导数，则当x≠0时，f’(x)=______。
参考答案：-2sinx-xcosx
解析：[详解] 令u=tx，则有[*]于是
[*]
即[*]
两边对x求导，f(x)=f(x)+xf’(x)+2xsinx+x2cosx，x≠0
故 f’(x)=-2sinx-xcosx