参考答案：

此类题首先要理清MC、AC、AVC，理清了它们，分析起来就方便多了。

(1)产量为正的要求是MC≥AVC，我们可以根据MC＝AVC来分析：

由C₁＝18+2q²+20q可知：MC₁=-4q+20，AVC₁＝2q+20

由MC₁=AVC₁得：4q+20＝2q+20g_min＝0p₁=AVC₁＝20

由C₂＝25+q²可知：MC₂=2q，AVC₂＝q

由MC₂=AVC₂得：2q＝q＞q_min＝0p₂=AVC₂＝0

由C₃+12+3q²+5q可知：MC₃＝6q+5，AVC₃＝3q+5

由MC₃=AVC₃得：6g+5＝3g+5q_min＝0p₃=AVC₃＝5

只有市场价格p≥max(p₁，P₂，P₃)＝20时，才可能三家企业都选择短期生产，即产量都为正。

(2)如果0≤市场价格p＜5，市场上只有企业2生产，此时供给曲线Q＝q₂＝

如果5≤市场价格p＜20，企业2与企业3都会生产，此时供给曲线Q＝q₂+q₃＝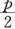

如果市场价格p≥20，三家企业都会生产，此时供给曲线Q＝q₁+q₂+q₃＝

所以，短期市场供给曲线为：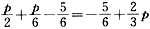

容易看出该完全竞争行业为成本递增行业，长期供给曲线理论上为向右上倾斜的曲线。

由于完全竞争行业不存在超额利润，长期成本高的厂商如果不能使MC＝P则会退出，剩下的是满足MC＝P的厂商，或者由于厂商增多引起行业MC上升，连MC最低的厂商也不能满足MC＝P。考虑这两种情况的长期供给曲线为：

Q＝0，或Q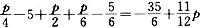＝，p≥0。