假定q为产量，垄断生产者S采用成本函数为CA（q）＝10+8q的技术A或成本函数为CB（q）＝60+2q的技术B进行生产，相应商品的市场需求函数为P＝24-Q，P与Q为市场价格与市场需求。试求：
（1）若垄断生产者S的市场垄断地位始终不可能受到威胁，则S公司应该采用何种生产技术（需要具体说明理由）。
（2）若垄断生产者S采用问题（1）选择的技术进行生产，生产相同商品的竞争对手T采用成本函数为C（q）＝F+7q的技术进人生产者S垄断的市场并与之展开竞争，F为某个常数，生产者S与T的竞争遵循古诺（Cournot）模式，则该商品的市场价格为多少生产者S与T的利润各为多少F的取值范围如何
参考答案：
生产者S的总收益为：
TR=P·Q＝(24-Q)Q
边际成本为：MR＝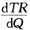
＝24-2Q
技术A：MC=C’A(q)＝8，根据MR=MC条件有：24-2Q=8
Q＝8，于是，利润π＝TR-TC＝(24－8)×8－(10+8×8)=54
技术B：MC=C’B(q)＝2，根据MR=MC有：24-2Q＝2
Q＝11，利润π＝TR-TC=61
对比两种技术的利润可知，采用技术B会获得更多的利润。所以，生产者肯定会采用B技术。
(2)市场需求函数为：P＝24-(QS+QT)
对于厂商S有利润函数为：
πs＝TRs-TCs＝P·QS-(60+2QS)
＝[24-(QS+QT)]QS-(60+2QS)
＝22QS-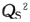
-QSQT-60
利润最大化的一阶条件是：
＝22-2QS-QT＝0 (1)
对于厂商T有利润函数为：
πT＝TRT-TCT＝P·QT-(F+7QT)
＝[24-(QS+GT)]GT-(F+7QT)
＝17QT-QSQT-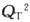
-F
利润最大化的一阶条件是：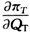
＝17-2QT-QS＝0 (2)
把这两个方程联立求解，可求得：QS=9，QT＝4。
从而求得：价格P＝11。
把QS的值代入得S的利润方程可求得：S的利润πS＝21；我们用同样的办法也可求得T的利润πT＝16-F。
要使T进入行业参与竞争必然要求T的利润πT≥0，也就是：16-F≥0，从而可以求得F≤16，当然，F是不小于0的，所以F的取值范围为0≤F≤16。