问题
问答题
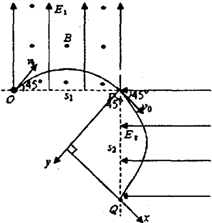
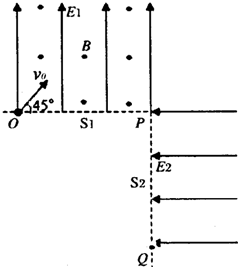
如图所示,竖直平面上有相互垂直的匀强电场和匀强磁场,电场强度E1=2500N/C,方向竖直向上;磁感应强度B=103T,方向垂直纸面向外;有一质量m=1×10-2kg、电荷量q=4×10-5C的带正电小球自O点沿与水平线成45°以v0=4m/s的速度射入复合场中,之后小球恰好从P点进入电场强度E2=2500N/C,方向水平向左的第二个匀强电场中.不计空气阻力,g取10m/s2.
求:(1)O点到P点的距离s1;
(2)小球经过P点的正下方Q点时与P点的距离s2.
答案
(1)带电小球在正交的匀强电场和匀强磁场中受到重力G=mg=0.1N;
电场力F1=Eq=0.1N
即G=F1,故小球在正交的电场由A到C做匀速圆周运动.
根据牛顿第二定律可知Bqv0=mv 20 R
解得:R=
=1mmv0 Bq
由几何关系得:s1=
R=2
m; 2
(2)带电小球在C点的速度大小仍为v0=4m/s,方向与水平方向成45°.
由于电场力F2=Eq=0.1N
与重力大小相等,方向相互垂直,
则合力的大小为F=0.1
N,方向与初速度垂直,故小球在第二个电场中作平抛运动.2
建立如图所示的坐标系,沿y方向上,小球的加速度a=
=10F m
m/s2; 2
位移y=
at21 2
x方向上有小球的位移x=v0t
由几何关系可知:y=x
即
at2=v0t,1 2
解得:t=0.4
s2
由几何关系可知,Q到P点的距离为s2=
x=3.2m.2