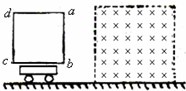
如图所示,光滑水平面停放一小车,车上固定一边长为L=0.5m的正方形金属线框abcd,金属框的总电阻R=0.25Ω,小车与金属框的总质量m=0.5kg.在小车的右侧,有一宽度大于金属线框边长,具有理想边界的匀强磁场,磁感应强度B=1.0T,方向水平且与线框平面垂直.现给小车一水平速度使其向右运动并能穿过磁场,当车上线框的ab边刚进入磁场时,测得小车加速度a=10m/s2.求:
(1)金属框刚进入磁场时,小车的速度为多大?
(2)从金属框刚要进入磁场开始,到其完全离开磁场,线框中产生的焦耳热为多少?
(1)设小车初速度为v0,则线框刚进入磁场时,ab边由于切割磁感线产生的电动势为:
E=BLv0…①
回路中的电流:I=
…②E R
根据牛顿定律:BIL=ma…③
由以上三式可解得:v0=5m/s
(2)设线框全部进入磁场时小车速度为v1,进入过程平均电流为
,所用时间为△t,则. I
=. I
=△Φ R△t
…④BL2 R△t
根据动量定理得
-B
L△t=mmv1-mv0…⑤. I
解得:v1=4m/s
设线框离开磁场时小车速度为v2,进入过程平均电流为
,所用时间为△t1,则:. I1
=. I1
=△Φ R△t1
…⑥BL2 R△t1
根据动量定理得
-B
L△t1=mv2-mv1…⑦. I1
解得:v2=3m/s
线框从进入到离开产生的焦耳热应等于系统损失的机械能,即:
Q=
m1 2
-v 20
m1 2
=4.0Jv 22
答:
(1)金属框刚进入磁场时,小车的速度为5m/s.
(2)从金属框刚要进入磁场开始,到其完全离开磁场,线框中产生的焦耳热为4.0J.
